


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil
La prise en compte de la variabilité des paramètres de sol par l’intermédiaire de variables aléatoires peut être effectuée par de nombreuses méthodes. Néanmoins, ce genre d'étude est conduite en négligeant la variabilité spatiale des paramètres de sol, c'est-à-dire en considérant que le sol est sujet à variabilité mais reste homogène. Cette hypothèse forte opère un lissage de propriétés du sol et est donc de nature à occulter certains phénomènes liés aux hétérogénéités naturelles qu’a pu produire l’histoire géologique parfois tourmentée des sites considérés. Il est pourtant possible d’étudier l’impact de cette variabilité spatiale sur le comportement des ouvrages géotechniques. On présente ici un exemple d'étude de la stabilité à l’effondrement en sol purement frottant d’un front de taille pressurisé. La théorie des champs aléatoires est utilisée pour modéliser les variations spatiales de l’angle de frottement interne du sol.
Un modèle bidimensionnel d’effondrement du front est développé dans le cadre du théorème cinématique de l’analyse limite. Ce modèle est une simplification en deux dimensions du modèle 3D d'effondrement publié dans Mollon et al. (2011). Il permet de prendre en compte la variabilité spatiale du sol pour des temps de calcul nettement plus réduits que ceux d’un modèle numérique. Ce mécanisme d’effondrement analytique est validé par une série de comparaisons avec les résultats fournis par un modèle numérique programmé sous le logiciel Flac.
Cette validation est effectuée successivement en sol homogène, puis de manière systématique en sol hétérogène (par l’introduction de faiblesses localisées dans le massif de sol, puis par modélisation de la variabilité spatiale sous forme de champs aléatoires 2D). Il apparaît que le modèle analytique permet de représenter avec une précision satisfaisante l’impact des hétérogénéités de terrain sur la forme de la rupture et sur la pression limite d’effondrement.
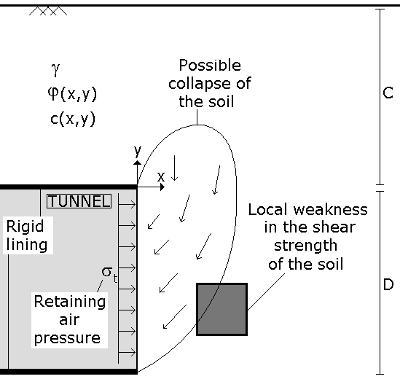
Figure 1. Position du problème : stabilité d'un front de taille en présence d'un sol spatialement variable ou d'une faiblesse localisée.
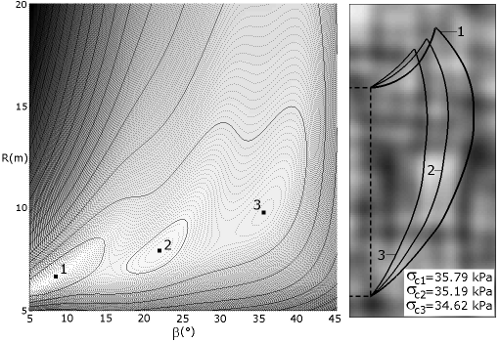
Figure 3. Optimisation des paramètres géométriques du mécanisme. En présence d'une variabilité spatiale, on observe des optimums locaux (points 2 et 3). Sous certaines conditions, ceci peut conduire à des ruptures multiples.

Figure 5. Validation quantitative du modèle d'analyse limite en présence d'une faiblesse localisée en pied de front de taille.

Figure 2. Principe du modèle 2D : les lignes de glissement inférieure et supérieure sont discrétisées en segments de façon à respecter localement la règle de normalité (angle entre la ligne de glissement et le champ de vitesse égal à la valeur locale de l'angle de frottement interne du sol).
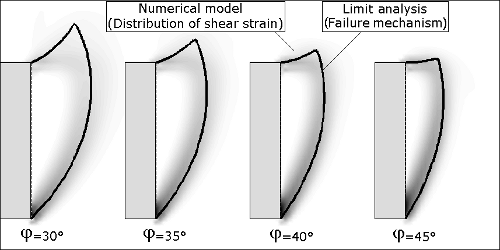
Figure 4. Comparaison entre les faciès d'effondrement fournis par le mécanisme 2D et par un modèle numérique.
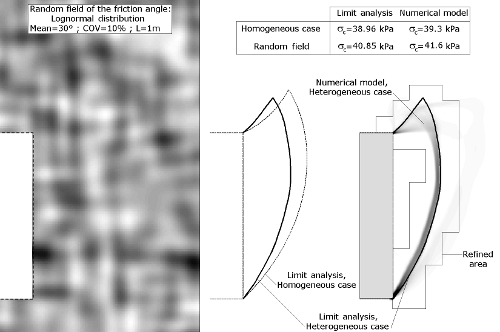
Figure 6. Exemple de validation en présence d'un champ aléatoire. Comparé à un modèle numérique, le mécanisme 2D décrit très bien les nouvelles lignes de glissement et le changement de la pression limite ultime.