


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Associate Professor
National Institute for Applied Sciences of Lyon
PhD, Civil Engineering, INSA Lyon
HDR, INSA Lyon



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Associate Professor
National Institute for Applied Sciences of Lyon
PhD, Civil Engineering, INSA Lyon
HDR, INSA Lyon
Several methods exist that make it possible to account for the variability of soil parameters based on random variables. However, such studies have the drawback of disregarding the spatial variability of the soil parameters, i.e. of considering that the soil mass is subjected to variability but remains homogeneous. This assumption is very strong and may lead to ignoring some phenomena related to the natural heterogeneities that were produced by the geological history of a given site. However, it is possible to study the influence of this spatial variability on the behavior of geotechnical projects by other means. Such a study is presented here in the framework of the analysis of stability of a pressurized tunnel face in a purely frictional soil. The random fields theory is applied to simulate the spatial variations of the friction angle of the soil.
A 2D model of face collapse is developped in the framework of the kinematic theorem of limit analysis. This model is a 2D simplification of the 3D collapse mechanism published in Mollon et al. (2011). It makes it possible to account for the spatial variability in the soil mass, for computation times which are much smaller than the ones of a numerical model. This analytical collapse mechanism is validated by a large number of comparisons with the results provided by a numerical model of reference programmed in the commercial code Flac.
This validation is first performed in homogeneous soils and then in a systematic way in heterogeneous soils (by introducing some localised weaknesses in the soil mass, and then by simulating the spatial variability with 2D random fields). It appears that the analytical model provides a satisfactory assessment of the influence of soil heterogeneities on the collapse shape and on the critical collapse pressure.

Figure 1. Description of the problem : stability analysis of a pressurized tunnel face in the case of a localized soil weakness or of a spatially varying soil.
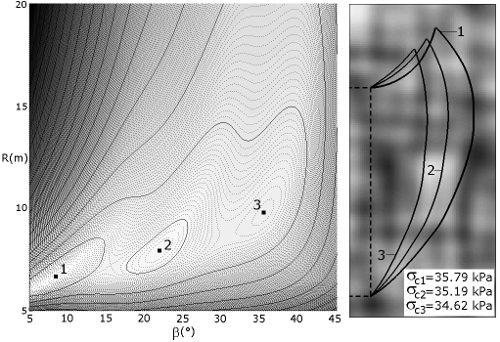
Figure 3. Optimisation of the geometrical parameters of the mechanism. In the case of a spatial variability, we can observe local optimums (points 2 and 3). Under certain conditions, this may lead to multiple failures.

Figure 5. Quantitative validation of the limit analysis model in the case of a localized weakness at the foot of the tunnel face.

Figure 2. Principle of the 2D model: the lower and upper slip lines are discretized by segments in order to fulfill locally the normality condition (angle between the slip line and the velocity field equal to the local value of the friction angle).
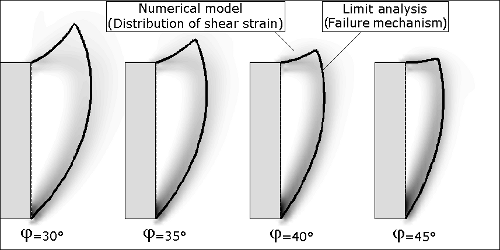
Figure 4. Comparison between the failure shapes provided by the 2D mechanism and by a numerical model.
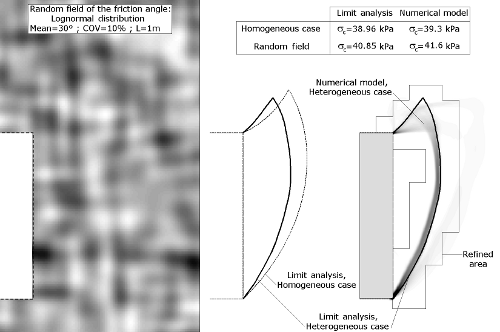
Figure 6. Example of validation in the case of a random field. Compared to a numerical model, the 2D mechanism describes fairly well the new slip lines and the modification of the critical collapse pressure.