


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil
Dans le cadre de l'aménagement des zones montagneuses, il est nécessaire de disposer d'outils de prédiction des zones à risques vis-à-vis des avalanches rocheuses. Les moyens de calcul actuels permettent d'envisager une méthode de simulation numérique de la propagation d'une masse rocheuse le long d'une pente naturelle, en utilisant la méthode des éléments discrets. Cette méthode repose sur un schéma de résolution explicite en pas de temps des équations du mouvement de Newton, combiné à des lois de contact prescrivant les efforts répulsifs se développant entre les différents solides en fonction de leur interpénétration. Dans la modélisation choisie, chaque élément de l'avalanche rocheuse est modélisé par un sphéro-polyèdre, ce qui simplifie grandement la détection des contacts et le calcul des forces répulsives. Dans le cadre des avalanches rocheuses (et des écoulements granulaires en général), il est apparu intéressant d'accorder beaucoup d'importance à la forme des blocs, mais de simplifier autant que possible la loi de contact. Il semble en effet difficile de reproduire dans toute leur complexité l'ensemble des phénomènes physiques ayant lieu lors de chacun des innombrables chocs que compte une avalanche rocheuse (ce qui justifie de simplifier la loi de contact afin d'en faire une "boite noire" dont les résultats à l'échelle de l'écoulement seraient satisfaisants), tandis que la forme et la taille des blocs sont des paramètres déterminants de l'écoulement. Une loi à quatre paramètres (raideurs normale et tangentielle du contact, coefficient de frottement, et coefficient d'amortissement normal) a donc été choisie de manière à avoir un contrôle précis des différentes sources de dissipations énergétiques au sein de l'écoulement.
Avant de s'intéresser à un cas réel en contexte naturel, la pertinence du modèle a été évaluée en le confrontant aux résultats expérimentaux de Manzella et Labiouse (2009). Leurs expériences consistaient à mettre en place un assemblage de petites briques (d'une longueur de 3cm et au nombre de 6000 à 10000), et de relâcher cet assemblage sur un biplan de manière à observer l'écoulement de la masse granulaire sur la pente et son dépôt sur le plan horizontal. L'estimation des paramètres de contact a été effectuée à partir d'expériences additionnelles utilisant les matériaux d'origine des expériences de Manzella et Labiouse (briques et support). Des essais de rebond de briques ont été réalisés, avec prises de vues par deux caméras rapides. Une analyse inverse des trajectoires de chute libre et de rebond a permis de définir un jeu de huit paramètres de contact (quatre paramètres pour le contact brique-pente, et quatre paramètres pour le contact inter-briques), qui ont ensuite été introduits dans la simulation de l'évènement complet. Les résultats de cette simulation (vitesses de propagation et de dépôt, forme et taille du dépôt granulaire) ont montré une excellente correspondance avec les résultats expérimentaux, et ont prouvé que le comportement collectif d'une masse granulaire en écoulement pouvait être modélisé à partir de lois de contact très simples calibrées sur des impacts isolés.
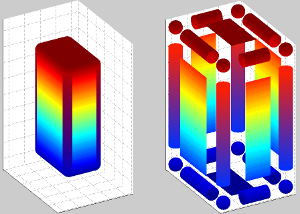
Figure 1. Stratégie de modélisation par sphéro-polyèdre : chaque coin est représenté par une sphère, et chaque arète par un cylindre.

Figure 3. Prises de vues de la même expérience par deux caméras rapides (a. et b.).
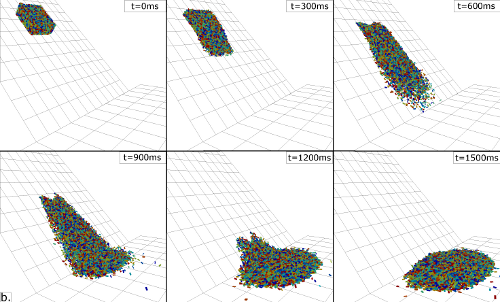
Figure 5. Modélisation de l'expérience de Manzella et Labiouse (2009), de l'assemblage dans la boîte de départ au dépôt final sur le plan horizontal.
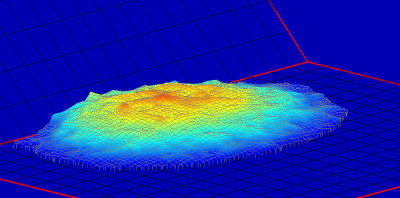
Figure 7. Enveloppe non-convexe du dépôt final, permettant par exemple d'estimer son volume.

Figure 2. Loi de contact simple à quatre paramètres. La dissipation d'énergie est introduite par frottement, et par un coefficient de dissipation normale décrivant le rapport entre les raideurs de chargement et de déchargement.

Figure 4. Détermination des paramètres de contact par rétro analyse sur les deux caméras (a. et b.). De gauche à droite : prises de vues, détermination de la trajectoire 3D, meilleure représentation numérique de l'impact.
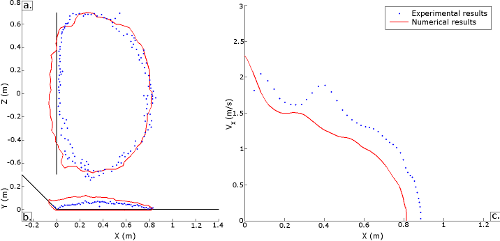
Figure 6. Comparaison entre les résultats expérimentaux et numériques, en termes de formes du dépôt (a. et b.) et de vitesse du front de l'avalanche (c.). Les résultats sont jugés très satisfaisants compte tenu du fait que les paramètres de contact ont été calibrés sur des essais additionnels et non par rétro-analyse de l'évènement complet.
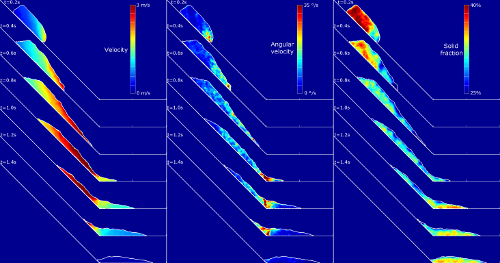
Figure 8. Techniques d'interpolation utilisées pour tracer les champs continus de grandeurs d'intérêt, telles que la vitesse et la vitesse angulaire des particules ou la densité locale de l'assemblage granulaire.