


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil
Dans le cadre de l’excavation d’un tunnel à faible profondeur en site urbain, l’ingénieur se trouve confronté à plusieurs défis. L'un des plus importants est de garantir la stabilité du front de taille du tunnel lors de son excavation afin d’assurer la sécurité des ouvriers et d’empêcher des phénomènes dangereux en surface (tels que des fontis ou des refoulements de sol). Il est donc nécessaire de disposer de modèles de prédiction fiables pour estimer le domaine de pression admissible au front de taille. Celle-ci ne doit être ni trop faible (afin de prévenir un effondrement du front) ni trop élevée (afin de prévenir un refoulement en surface).
Plusieurs modèles analytiques de complexité croissante ont été développés à partir du théorème cinématique de l’analyse limite. En sol frottant et/ou cohérent, le mécanisme nommé M1 propose une extension à cinq blocs du mécanisme classique à deux blocs de Leca et Dormieux [1990]. Une méthode de discrétisation spatiale permet de générer la surface externe du mécanisme M2, qui est basé sur les mêmes principes que le mécanisme M1 (plusieurs blocs rigides en translation), mais permet de s’affranchir de son principal défaut (intersection incomplète entre le front de taille et le premier bloc). Le mécanisme M3 permet de se rapprocher encore plus des formes de rupture observées numériquement, en adoptant à un champ de vitesse cylindrique une méthode de discrétisation comparable à celle de M2. Les mécanismes M4 et M5 sont développés à partir de concepts issus de Klar et al. [2007] afin de s’approcher au mieux d’une rupture par déformation continue du massif de sol sans discontinuité de vitesse, telle qu’elle est généralement observée en sol purement cohérent. Une comparaison avec les résultats numériques montre que le mécanisme M3 fournit de bonnes estimations des pressions limites en sol frottant, mais n’obtient pas de bons résultats en sol purement cohérent. Le mécanisme M5, en revanche, constitue une amélioration très sensible des approches existantes en sol purement cohérent. Ces résultats confirment qu’un modèle basé sur le théorème cinématique de l’analyse limite est d’autant plus performant que le champ de vitesse postulé est proche des observations numériques et expérimentales. On dispose donc désormais de deux modèles analytiques permettant d’estimer de manière fiable les pressions limites d’effondrement et de refoulement dans tout type de sol frottant et/ou cohérent, pour des temps de calcul réduits.
Le travail en cours consiste à étendre ces approches à des cas plus complexes, tels que des critères de rupture non-linéaires ou des fronts de taille renforcés.

Figure 1. a. Mécanisme d'effondrement de Leca et Dormieux (1990), composé de deux blocs coniques en translation ; b. Mécanisme M1, adaptation à 5 blocs (Mollon et al. 2009) ; c. Mécanisme M2, discrétisation spatiale de trois blocs en translation, pour prendre en compte la totalité du front de taille (Mollon et al. 2010).
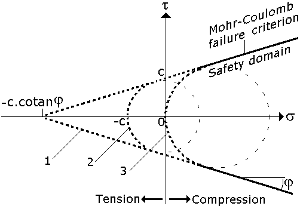
Figure 3. Critères de Mohr-Coulomb tronqués en traction, pour améliorer les résultats en présence d'un sol frottant et cohérent.

Figure 5. Mécanismes de refoulement du sol en avant du front de taille ; d. Mécanisme de Leca et Dormieux (1990) ; e. Mécanisme M1 (Mollon et al. 2009).

Figure 7. Mécanismes d'effondrement fondés sur des mouvements rigidifiants et appliqués à un sol purement cohérent ; a. Mécanisme M1 ; b. Mécanisme M2 ; c. Mécanisme M3 ; Aucun de ces modèles ne donne de résultat satisfaisant en sol non frottant.

Figure 9. Champ de vitesse du mécanisme M5 dans le plan de symétrie du tunnel. Ce mécanisme améliore considérablement les estimations de la pression d'équilibre par rapport aux modèles rigidifiants.
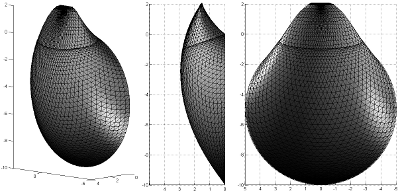
Figure 2. Mécanisme d'effondrement M3, fondé sur un champ de vitesse rotationnel et une discrétisation spatiale de la surface de glissement (Mollon et al. 2011). Ce mécanisme est à ce jour celui qui fournit la meilleure estimation par l'extérieur de la pression limite d'effondrement en sol frottant.
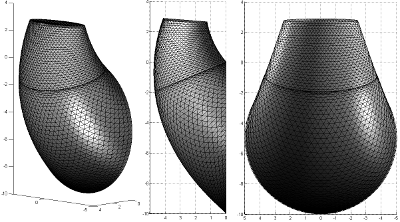
Figure 4. Mécanisme M3 adapté au critère MC modifié. La partie supérieure du mécanisme est tronquée, avec prise en compte d'une dissipation énergétique liée également à la traction et non plus seulement au cisaillement.

Figure 6. Mécanisme rotationnel de refoulement M3 (Mollon et al. 2011).

Figure 8. Enveloppe des mécanismes M4 et M5 d'effondrement en sol purement cohérent. Ces mécanismes reposent sur un champ de taux de déformation continu, sans saut de vitesse.

Figure 10. Maillage DF utilisé par les mécanismes M4 et M5 pour le calcul de la dissipation d'énergie dans le champ de taux de déformation.