


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Associate Professor
National Institute for Applied Sciences of Lyon
PhD, Civil Engineering, INSA Lyon
HDR, INSA Lyon



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Associate Professor
National Institute for Applied Sciences of Lyon
PhD, Civil Engineering, INSA Lyon
HDR, INSA Lyon
In the framework of a tunnel excavation in urban context, engineers are confronted to several challenges. Not the least is to maintain the stability of the tunnel face during its excavation in order to ensure the safety of the workers and to prevent dangerous phenomenas at the ground surface. It is thus necessary to build up predictive models in order to assess the admissible retaining pressure interval to be applied to the tunnel face. This pressure should be neither too small (to prevent face collapse) nor too high (to prevent face blow-out towards the ground surface).
Several analytical models of growing complexity have been developped based on the kinematic theorem of the limit analysis theory. In a frictional and/or cohesive soil, the so-called M1 mechanism proposes an extension to 5 blocs of the classical 2-blocs mechanism by Leca and Dormieux [1990]. A spatial discretization technique makes it possible to generate the external surface of the M2 mechanism, which is based on the same principles than the mechanism M1 (several rigid block in translation), but suppresses its main drawback (incomplete intersection between the tunnel face and the first block). The M3 mechanism makes it possible to get even closer to the actual failure shapes observed numerically, by adopting a cylindrical velocity field and a discretization method similar to the one of M2. Mechanisms M4 and M5 are developped from concepts introduced by Klar et al. [2007], in order to represent a failure by continuous deformation of the soil mass behind the tunnel face without any velocity jump, as it is commonly observed in purely cohesive soils. A comparison with numerical results shows that the M3 mechanism provides satisfactory estimations of the critical face pressures in frictional soil, but is not accurate in purely cohesive soils. However, the M5 mechanism provides a consistent improvement of the existing approaches in purely cohesive soils. These results confirm that a model based on the kinematic theorem of limit analysis is much more accurate when the postulated velocity field is close to numerical and/or experimental observations. With this work, we now have two mechanisms which allow a reliable computation of the critical collapse and blow-out pressures in any type of frictional and/or cohesive soil, for limited computation times.
On-going work is currently dedicated to the extension of these mechanisms to more complicated contexts, such as non linear failure criterions or reinforced tunnel faces.

Figure 1. a. Collapse mechanism by Leca et Dormieux (1990), composed by two blocks in translation ; b. M1 mechanism, adaptation to 5 blocks (Mollon et al. 2009) ; c. M2 mecanism, Spatial discretization of three translating blocks, to account for the totality of the tunnel face (Mollon et al. 2010).
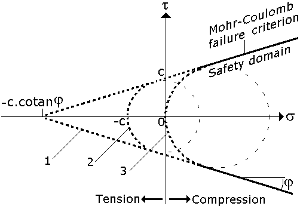
Figure 3. Truncated Mohr-Coulomb criterion, In order to improve the mechanism preformance in frictional and cohesive soils.

Figure 5. Face blow-out mehcanisms ; d. Mecanism of Leca and Dormieux (1990) ; e. M1 mecanism (Mollon et al. 2009).

Figure 7. Collapse mechanisms based on rigid-blocks motions, but applied to purely cohesive soils ; a. M1 mecanism ; b. M2 mecanism ; c. M3 mecanism ; None of these models provide satisfactory results in non-frictional soils.

Figure 9. Velocity field of the M5 mechanism in the plane of symmetry of the tunnel. This mechanism considerably improves the estimations of the critical pressures when compared to the rigid-blocks mechanisms.
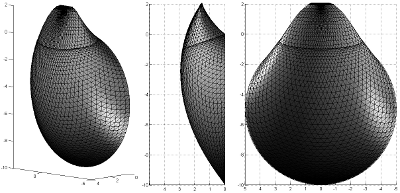
Figure 2. M3 collapse mecanism, based on a rotationnal velocity field and on a spatial discretization of the slip surface (Mollon et al. 2011). This mechanism provides, at the moment, the best estimation in the framework of the kinematic theorem of the critical collapse pressure in frictional soil.
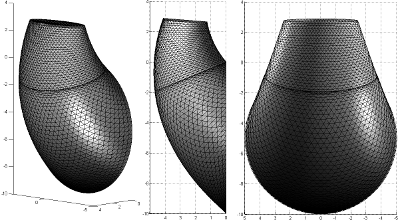
Figure 4. M3 mecanism adapted to the modified MC criterion. The upper-part of the mechanism is truncated, accounting for an energy dissipation related to traction, and not only to shearing.

Figure 6. Rotationnal mecanism M3 for face blow-out (Mollon et al. 2011).

Figure 8. Extrenal enveloppe of the collapse mechanisms M4 and M5 in purely cohesive soils. These mechanisms are based on a continuous field of deformation rate, without velocity jump.

Figure 10. Finite Differences mesh used in M4 and M5 mechanism for the computation of the energy dissipation in the field of strain rate associated to collapse.