


Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil



Guilhem MOLLON
guilhem.mollon@insa-lyon.fr
Maître de Conférences
Institut National des Sciences Appliquées de Lyon
Docteur - HDR (INSA Lyon)
Ingénieur INSA, Normalien, Agrégé de Génie Civil
De nombreux modèles déterministes d’étude de la stabilité d’un front de taille pressurisé existent dans la littérature. Les modèles numériques permettent d’obtenir à la fois une estimation satisfaisante des pressions limites d’effondrement et de refoulement, mais également des faciès de ruptures correspondant aux deux types d’instabilité. L'étude de différents modèles numériques programmés dans le logiciel commercial Flac3D démontre l’importance de la finesse du maillage et de la procédure de détermination de la pression limite. Les temps de calcul en jeu ne permettent pas d’envisager l’application des modèles numériques 3D dans un cadre probabiliste avec les moyens de calcul actuels, mais ils peuvent s’avérer très utiles pour la validation de modèles moins coûteux. Par ailleurs, ils permettent de mettre en lumière les différences de faciès de rupture apparaissant entre différents types de sols.
Les modèles numériques sont également très bien adaptés à l'étude des mouvements de sol induits par l’excavation d’un tunnel pressurisé. Le modèle présenté ici propose une modélisation relativement complexe de l’ensemble des phénomènes apparaissant autour du tunnelier lors de l’excavation. Il permet d’obtenir non seulement le tassement maximal, mais également un certain nombre d’autres grandeurs (pentes, déformations horizontales, etc.) présentant un intérêt dans leur impact possible sur un éventuel bâti en surface.
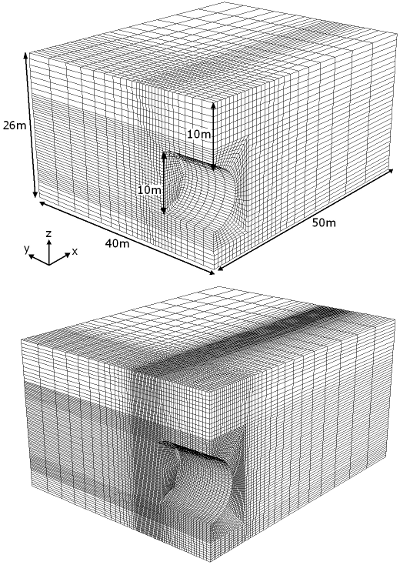
Figure 1. Modèles numérique d'étude de la stabilité d'un front de taille pressurisé, avec deux niveaux de maillage.
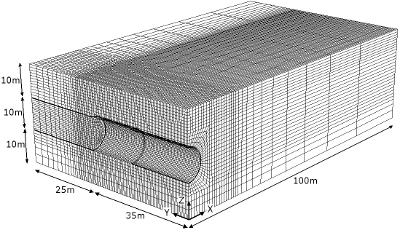
Figure 4. Modèle numérique d'étude des mouvements de sol induits par une excavation pressurisée.
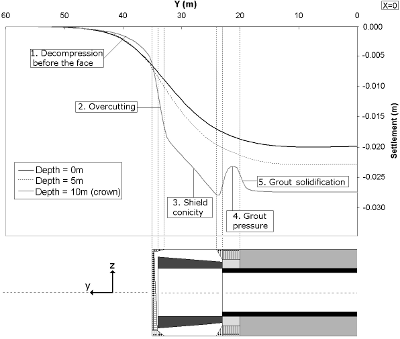
Figure 6. Allure des tassements observés après simulation. L'influence des différentes sources de tassement apparaît très clairement.
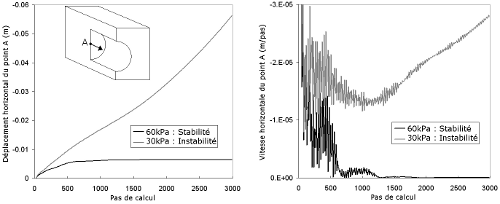
Figure 2. Procédure d'estimation de la pression d'équilibre à l'effondrement. Pour une pression donnée, l'état de stabilité est déterminé par l'étude du déplacement et de la vitesse d'extrusion du front de taille. La pression limite est déterminée par encadrements successifs lors d'une procédure de dichotomie.
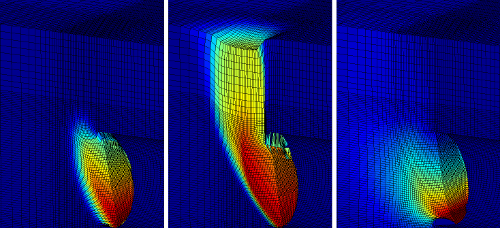
Figure 3. Faciès de rupture pour différents types de sol : de gauche à droite, sol frottant associé, sol frottant non dilatant, sol purement cohérent. Les différences de faciès sont très claires : les sols frottants font apparaître des zones de cisaillement localisées entre le bloc en mouvement et le sol au repos (avec ou sans "cheminée", selon la dilatance du sol), et les sols non frottants font apparaître un champ de déformations diffuses en arrière du front.
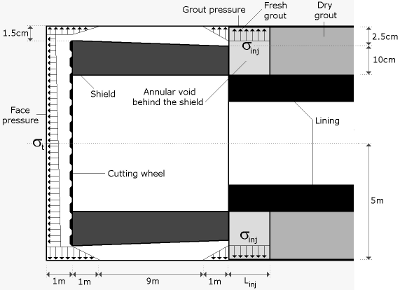
Figure 5. Schéma de principe du modèle, avec prise en compte de la pression de soutènement, de la surcoupe, de la migration de boue en arrière du bouclier, de la conicité de la jupe, de la pression d'injection en arrière de la jupe, et du durcissement du mortier de bourrage.
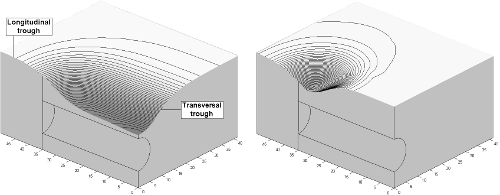
Figure 7. Cuvettes de tassement 3D ; à gauche, cuvette totale ; à droite, cuvette instantannée due au dernier pas d'excavation (échelle dilatée d'un facteur 10).